建平中学第一学期高中三年级数学9月月考
1、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答卷纸的相应地方直接填写结果.
1.函数![]() 的最小正周期为________.
的最小正周期为________.
2.设复数![]() ,
,![]() 为虚数单位,则
为虚数单位,则![]() ________.
________.
3.已知全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]() ___.
___.
4.正实数![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的最大值为________.
的最大值为________.
5.已知函数![]() ,
,![]() 是函数
是函数![]() 的反函数,若
的反函数,若![]() 的图像过点
的图像过点![]() ,则
,则![]() 的值为________.
的值为________.
6.设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,
,![]() ,则
,则![]() ________.
________.
7.若行列式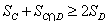 中的元素
中的元素![]() 的代数余子式的值等于
的代数余子式的值等于![]() ,则实数
,则实数![]() 的取值集合为________.
的取值集合为________.
8.不等式组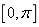 所表示的地区的面积为________.
所表示的地区的面积为________.
9.将函数![]() 的图像向右平移
的图像向右平移![]() 个单位得到函数
个单位得到函数![]() 的图像,若存在
的图像,若存在![]() 使得
使得![]() ,则
,则![]() 的最小值为________.
的最小值为________.
10.在![]() 的展开式中任取两项,其系数的乘积是偶数的概率为________.
的展开式中任取两项,其系数的乘积是偶数的概率为________.
11.设![]() 、
、![]() 分别是抛物线
分别是抛物线![]() 和圆
和圆![]() 上的点.若存在实数
上的点.若存在实数![]() 使得
使得![]() ,则
,则![]() 的最小值为________.
的最小值为________.
12.已知![]() ,函数
,函数![]() 在区间
在区间![]() 上有两个不同零点,则
上有两个不同零点,则![]() 的取值范围是________.
的取值范围是________.
2、选择题(本大题共有4题,满分20分,每题5分)每题有且只有一个正确选项.考生应在答卷纸的相应地方,将代表正确选项的小方格涂黑.
13.直线![]() 的一个法向量为( ).
的一个法向量为( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14.已知![]() 是空间两个不一样的平面,则“平面
是空间两个不一样的平面,则“平面![]() 上存在不共线的三点到平面
上存在不共线的三点到平面![]() 的距离相等”是“
的距离相等”是“![]() ”的( ).
”的( ).
(A)充分非必要条件 (B)必要非充分条件 (C)充要条件 (D)非充分非必要条件
15.关于函数![]() 的说法中正确的是( ).
的说法中正确的是( ).
(A)![]() 是周期函数 (B)
是周期函数 (B)![]() 在
在![]() 上有最小值
上有最小值
(C)![]() 在
在![]() 上有零点 (D)
上有零点 (D)![]() 的图像是中心对称图形
的图像是中心对称图形
16.能使命题“给定![]() 个非零向量(可以相同),若其中任意
个非零向量(可以相同),若其中任意![]() 个向量之和的模等于另外
个向量之和的模等于另外![]() 个向量之和的模,则这
个向量之和的模,则这![]() 个向量之和为零向量”成为真命题的一组
个向量之和为零向量”成为真命题的一组![]() 、
、![]() 的值为( ).
的值为( ).
①![]() ,
,![]() ②
②![]() ,
,![]() ③
③![]() ,
,![]() ④
④![]() ,
,![]()
(A)①② (B)③④ (C)①③ (D)②④
3、解答卷(本大题共有5题,满分76分)解答下列各题需要在答卷纸的相应地方写出必要的步骤.
17.(本题满分14分,第1小题满分6分,第2小题满分8分)
如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,
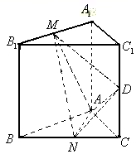
![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求点![]() 到平面
到平面![]() 之间的距离.
之间的距离.
18.(本题满分14分,第1小题满分6分,第2小题满分8分)
已知![]() .
.
(1)求![]() 的最大值及该函数获得最大值时
的最大值及该函数获得最大值时![]() 的值;
的值;
(2)在![]() 中,
中,![]() 分别是角
分别是角![]() 所对的边,若
所对的边,若![]() ,且
,且![]() ,
,
求边![]() 的值.
的值.
19.(本题满分14分,第1小题满分6分,第2小题满分8分)
某公司借助![]() 线上、线下门店线下销售商品
线上、线下门店线下销售商品![]() ,商品
,商品![]() 在上市
在上市![]() 天内全部售完.据统计,线上日销量
天内全部售完.据统计,线上日销量![]() 、线下日销量
、线下日销量![]() (单位:件)与什么时候上市的
(单位:件)与什么时候上市的![]()
![]() 天的关系满足:
天的关系满足:![]() ,
,![]()
![]() ,商品
,商品![]() 每件的销售收益为
每件的销售收益为![]() (日销量
(日销量![]() 线上日销量
线上日销量![]() 线下日销量).
线下日销量).
(1)设该公司商品![]() 的日销售收益为
的日销售收益为![]() ,写出
,写出![]() 的函数分析式;
的函数分析式;
(2)商品![]() 上市的哪几天给该公司带来的日销售收益高于
上市的哪几天给该公司带来的日销售收益高于![]() 元?
元?
20.(本题满分16分,第1小题满分4分,第2小题满分5分,第3小题满分7分)
给定椭圆![]() .过坐标原点的直线与
.过坐标原点的直线与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)求直线![]() 与直线
与直线![]() 斜率的乘积;
斜率的乘积;
(2)求证:![]() 是直角三角形;
是直角三角形;
(3)求![]() 面积的最大值.
面积的最大值.
21.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)
设![]() 是无穷正项等比数列,公比为
是无穷正项等比数列,公比为![]() .对于正整数集
.对于正整数集![]() 的子集
的子集![]() ,若
,若![]() ,概念
,概念![]() ;若
;若![]() ,概念
,概念![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)设![]() .若
.若![]() 、
、![]() 是
是![]() 的非空有限子集且
的非空有限子集且![]() ,求证:
,求证:![]() ;
;
(3)若对![]() 的任意非空有限子集
的任意非空有限子集![]() 、
、![]() ,只须
,只须![]() ,就有
,就有![]() ,求公比
,求公比![]() 的取值范围.
的取值范围.







